how to draw a phase diagram

Well, it can be sketched by knowing information such as the following:

• normal boiling point (#T_b# at #"one atm"#), if applicable
• normal melting indicate (#T_f# at #"1 atm"#)
• triple betoken (#T_"tp", P_"tp"#)
• disquisitional point (#T_c,P_c#)
• #DeltaH_"fus"#
• #DeltaH_"vap"#
• Density of liquid & solid

and by knowing where general phase regions are:

---

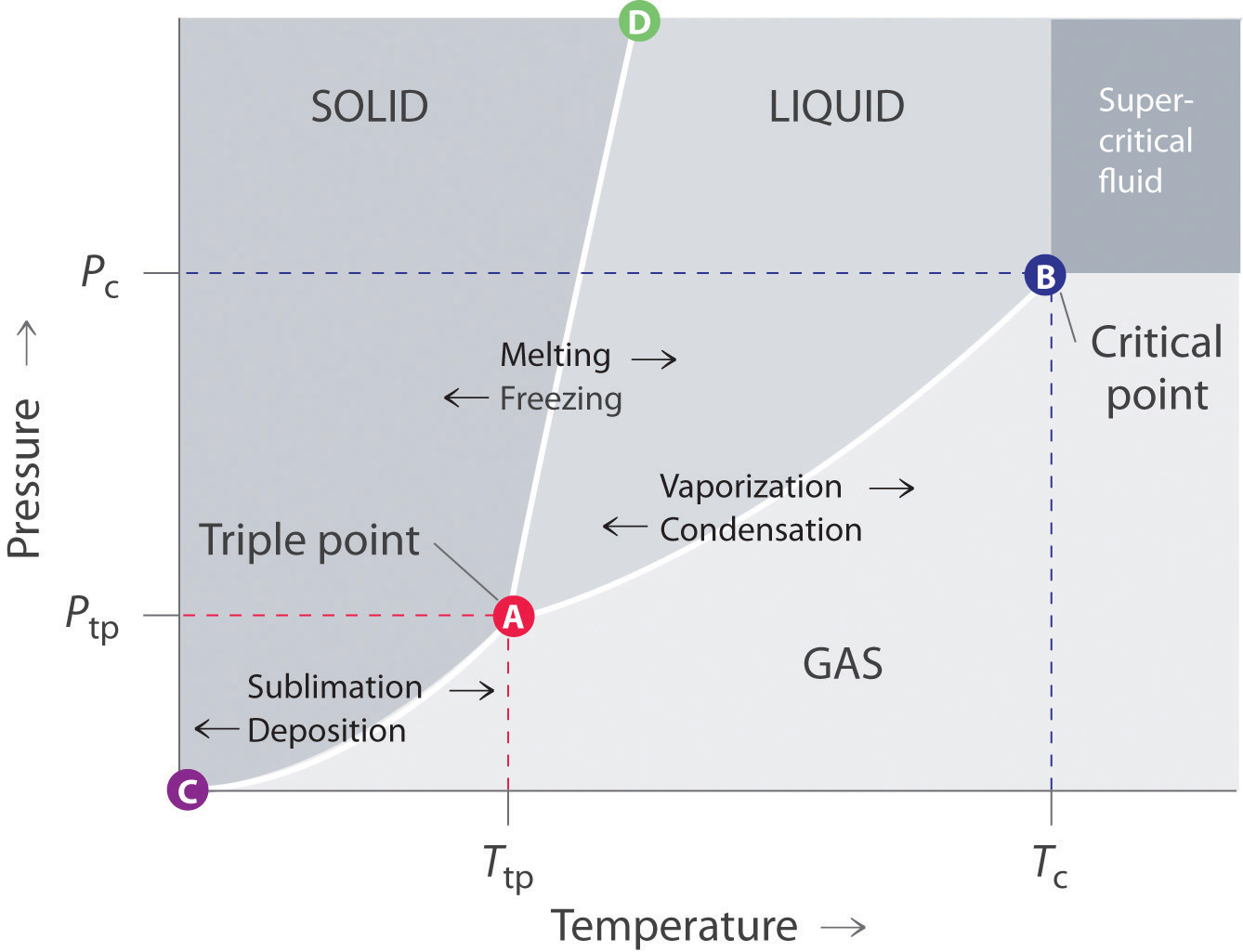
EXAMPLE DATA

Take #"CO"_2# equally an case. The post-obit data can exist institute on NIST:

• sublimation temperature: #"195 K"# (#-78.15^@ "C"#) at #"ane atm"#
• triple point: #"216.58 G"# (#-56.57^@ "C"#) at #"5.185 bar"# (#"5.117 atm"#)
• critical bespeak: #"304.23 K"# (#31.08^@ "C"#) at #"73.825 bar"# (#"72.860 atm"#)
• #DeltaH_"sub" = "25.ii kJ/mol"# at #"195 K"# (#-78.fifteen^@ "C"#) and #"1 atm"#
• Density of liquid is greater than density of solid
  #-># positive slope on the solid-liquid coexistence bend

DERIVING THE DIFFERENTIAL EQUATIONS

Next, consider the chemic potential #mu#, or the molar Gibbs' free energy #barG = Chiliad/northward#. Along a 2-stage coexistence curve, two phases are in equilibrium.

For example, suppose #"CO"_2# was sublimating. Then the solid and gas phases are in equilibrium and:

#mu_((southward)) = mu_((thou))#, or #barG_((s)) = barG_((m))#

From the Maxwell Relation for the Gibbs' complimentary energy, it follows that:

#dbarG_((yard)) - dbarG_((due south)) = dmu_((g)) - dmu_((due south)) = dDeltamu_((south)->(1000))#

#= -DeltabarS_"sub"dT + DeltabarV_"sub"dP = 0#

where #barS# and #barV# are the molar entropy and molar volume, respectively, of the stage change procedure, while #T# and #P# are temperature and force per unit area.

Therefore,

#DeltabarS_("sub")dT = DeltabarV_"sub"dP#

#=> (dP)/(dT) = (DeltabarS_"sub")/(DeltabarV_"sub")#

This gives the slope of the solid-gas coexistence bend. Obviously, the gas is less dense than the solid, and so the slope volition exist positive.

Now, the #DeltaH_"sub"# is improve known, so note that at a phase equilibrium, for some phase transition at constant temperature and pressure,

#DeltaG_"tr" = DeltaH_"tr" - T_"tr"DeltaS_"tr" = 0#,

and then

#DeltaS_"tr" = (DeltaH_"tr")/T_"tr"#.

Therefore, we obtain the Clapeyron differential equation:

#color(blue)((dP)/(dT) = (DeltabarH_"sub")/(T_"sub"DeltabarV_"sub"))#

And analogous equations can be derived for solid/liquid and liquid/vapor equilibria. The main departure is that for the liquid/vapor equilibrium, one tin can use the ideal gas police force to rewrite it as:

#(dP)/(dT) = (DeltabarH_"vap")/(T_bDeltabarV_"vap") = (DeltabarH_"vap"P_"vap")/(T_b cdot RT_b)#

Therefore, for the liquid/vapor phase equilibrium, nosotros have the Clausius-Clapeyron differential equation:

#1/P(dP)/(dT) = color(blue)((dlnP)/(dT) = (DeltabarH_"vap")/(RT_b^two))#

SOLVING THE DIFFERENTIAL EQUATIONS

This isn't that bad. In fact, all nosotros are typically looking for is whether the slope is positive or negative, and often it is positive (except for h2o freezing).

Solid/Gas, Solid/Liquid Equilibria

#(dP)/(dT) = ((+))/((+)(+)) > 0#

This equation typically isn't evaluated formally, except in small temperature ranges where it is approximately linear.

Simply if we were to solve it, we would demand an exceedingly pocket-sized temperature range . Provided that is the case,

#int_(P_1)^(P_2) dP = int_(T_1)^(T_2) (DeltabarH_"tr")/(DeltabarV_"tr")1/T_"tr"dT#

In this minor temperature range, #DeltabarH_"tr"# easily is constant, and and then is #DeltabarV_"tr"# (information technology can be calculated from known densities). So:

#color(blue)(DeltaP_"tr" ~~ (DeltabarH_"tr")/(DeltabarV_"tr")ln(T_(tr2)/T_(tr1)))#

Liquid/Vapor Equilibrium

#(dlnP)/(dT) = ((+))/((+)(+)^2) > 0#

This equation could be solved as a general chemical science practise, only not in this grade.

#int_(P_1)^(P_2) dlnP = int_(T_(b1))^(T_(b2))(DeltabarH_"vap")/R 1/T^2 dT#

Bold a minor-plenty temperature range that #DeltabarH_"vap"# does not vary,

#color(blue)(ln(P_2/P_1) = -(DeltabarH_"vap")/R[one/T_(b2) - ane/T_(b1)])#

And this is the better-known form of the Clausius-Clapeyron equation from full general chemistry. Information technology is used to notice boiling points at new pressures, or vapor pressures at new boiling points.

CONSTRUCTING THE PHASE DIAGRAM

The remainder is using the data one could become from using these equations on ane data point to get some other data point.

I generally start by plotting the triple point and disquisitional indicate, then outlining where the solid, liquid, and gas phase regions are. And then, I annotation which slopes are positive or negative, and sketch the curves from there.

#"CO"_2# has a phase diagram similar this:

• sublimation temperature: #"195 Chiliad"# (#-78.15^@ "C"#) at #"1 atm"#
• triple bespeak: #"216.58 Chiliad"# (#-56.57^@ "C"#) at #"5.185 bar"# (#"5.117 atm"#)
• critical point: #"304.23 Thousand"# (#31.08^@ "C"#) at #"73.825 bar"# (#"72.860 atm"#)

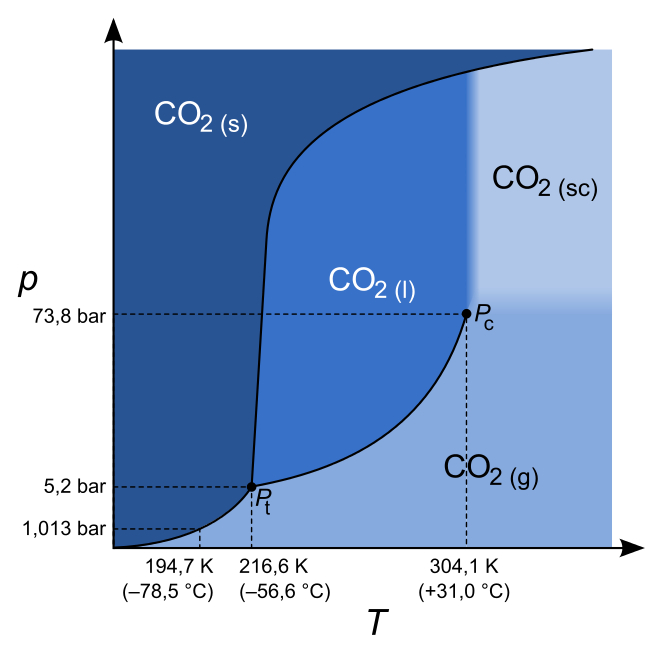
And equally you can see, all the slopes here are positive as predicted.

Source: https://socratic.org/questions/how-do-you-draw-phase-diagram-with-a-differential-equation

Posted by: francisviode1952.blogspot.com

Share this post