Where To Start Drawing A Bearing

Chapter thirteen: Bearing

Bearing is a manner of describing one object'southward position in relation to some other object. Information technology describes an object's position using the points of a compass.

Ships utilise bearing so the sailors know the exact position of a lighthouse or the harbour in relation to where they are. Aeroplanes employ begetting so the pilots know the exact position of the airfield, or which management they must wing. You could use bearing to describe the exact position of your school in relation to your home.

The photograph beneath shows a real compass that people use to discover bearings. In this affiliate, yous will find bearings using diagrams of a compass.

This compass is a different type of compass from the one you accept used when doing constructions.

The description has iii rules, which you volition learn about in this affiliate:

• Bearings are measured from the North line.
• Bearings are measured in a clockwise direction.
• Bearings are written as numbers with iii digits and a degree symbol.

If you follow these iii rules, you lot tin can describe the exact position of an object, and in that location will exist no confusion.

xiii.1 Cardinal points

When you utilise a map, or draw the position of a metropolis or a state, for example, yous can use bearings to give an indication of the the management in which someone would need to travel to get from one identify to another. These directions are based on the compass points N ( ), Southward ( ), Westward ( ) and East ( ).

If you await at a map of Nigeria, you will find that:

• Katsina is north of Kaduna
• Gombe is southward of Jobe
• Kogi is due west of Benue
• Edo is due east of Ondo.

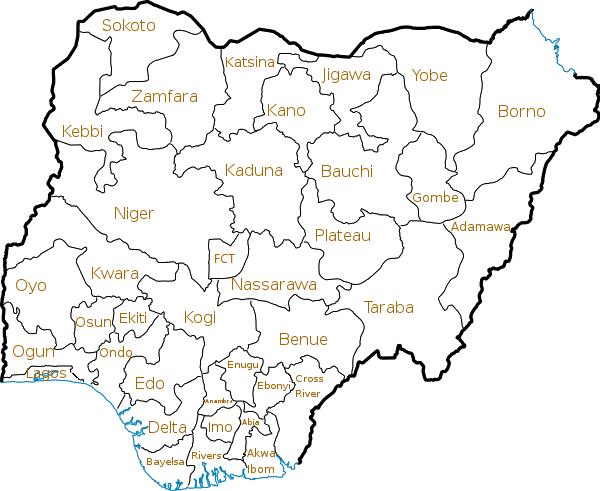
The four directions North, South, West and Due east are known as the major cardinal points.

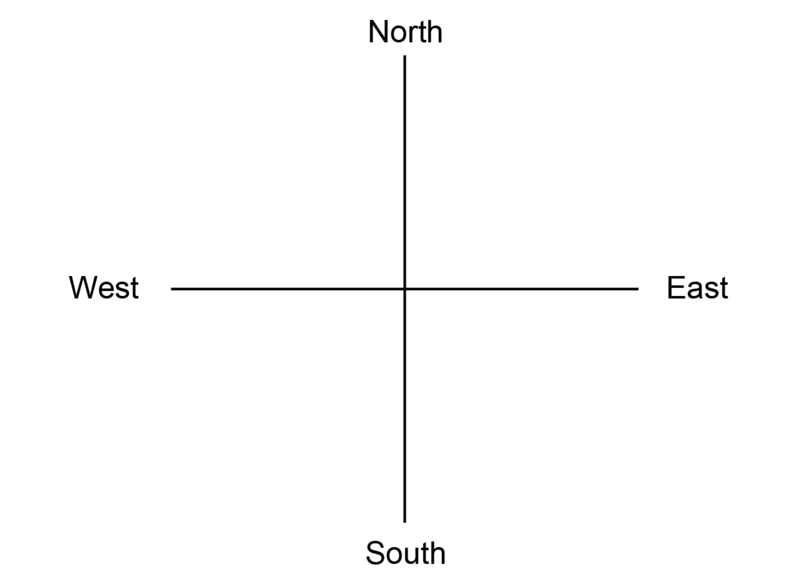
As the diagram below shows:

• N and South are in opposite directions on a vertical line
• West and East are in contrary directions on a horizontal line
• The North-Due south line is perpendicular to the West-Due east line.

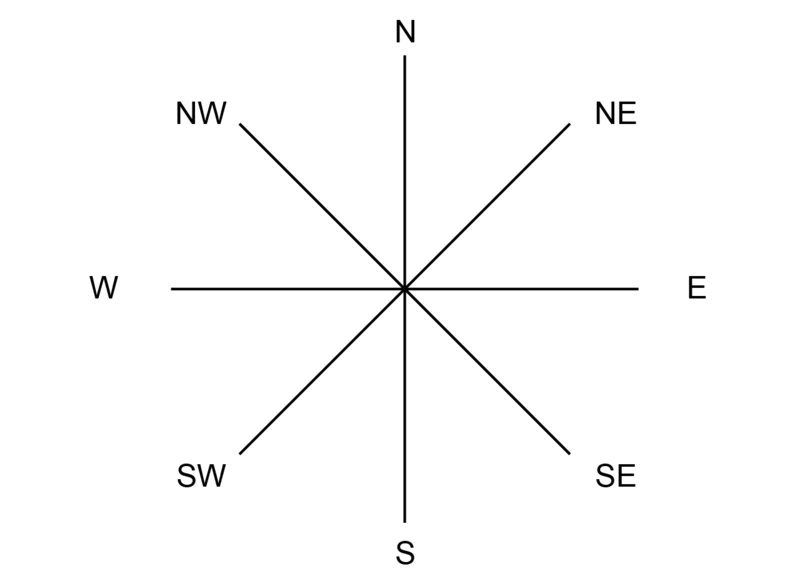
We can add two more than lines to the diagram to include the minor cardinal points:

• Due north-Eastward ( ) is midway between N and East
• South-East ( ) is midway between South and East
• North-Due west ( ) is midway between North and W
• South-West ( ) is midway betwixt South and West.

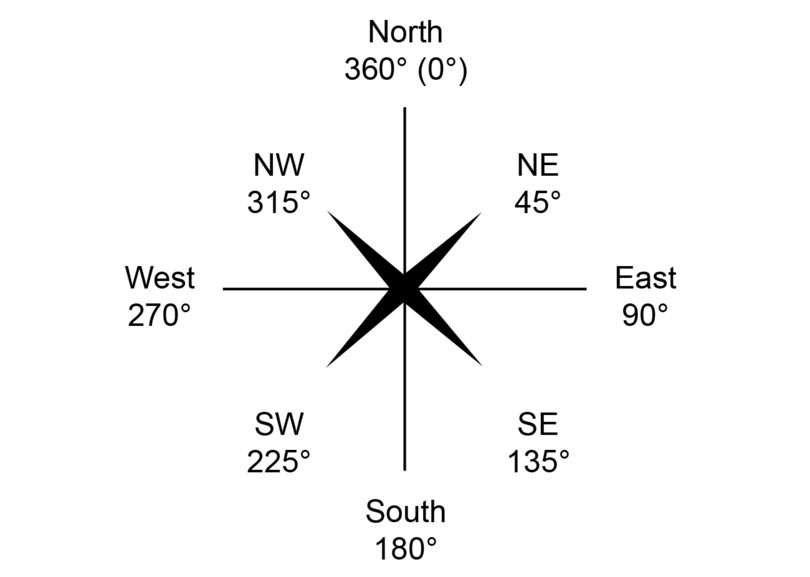
In working with begetting, y'all will need to measure angles from these cardinal points.

When yous measure the angles, you volition measure out in a clockwise direction.

To measure the angles, you need to begin at the North line, which is at . North is also at , because a full plow around the compass, which is called a revolution, is equal to .

major fundamental points The major cardinal points are North, South, West and East.

minor cardinal points The minor cardinal points are Due north-East, South-East, N-West and South-West.

clockwise direction The management in which the easily of a clock (or spotter) normally travel is the clockwise direction.

revolution A revolution is one full turn. A revolution is equal to .

Worked case thirteen.1: Working with the cardinal points

Using this diagram of a compass, answer the questions that follow.

1. Which primal signal is opposite West?
2. Which cardinal betoken is contrary North-Eastward?
3. At what angle do you observe South?
4. What primal point is at an angle of from North?

1. Step i: Refer to the diagram to identify W, and find what is opposite.

   East is contrary W.

2. Footstep 2: Refer to the diagram to place North-Due east, and detect what is contrary.

   Due south-Due west is opposite North-East.

3. Step 3: Refer to the diagram and identify Due south.

   S is at .

4. Step 4: Refer to the diagram and identify .

   North-West is at an angle of from North.

Exercise 13.1: Work with the cardinal points

1. Employ the map of the provinces of Nigeria to fill in the missing directions.

   

   1. Yobe is …. of Gombe.

   north

   1. Katsina is … of Zamfara.

   east

   1. Ogun is …. of Ondo.

   due west

   1. Delta is … of Edo.

   south

2. Draw your ain diagram to evidence the four major cardinal points.

   

3. Use your answer to Question 2. Add two more lines so that the diagram likewise shows the four minor cardinal points.

   

4. Which cardinal betoken is opposite East?

   West is reverse Due east.

5. Which key point is reverse North-W?

   South-East is opposite North-West.

6. At what angle do you find N-Due east?

   North-Eastward is at .

7. What cardinal point is at an bending of from North?

   Southward is at an angle of from North.

13.2 Finding bearings

Bearings are measured:

• from the North line
• in a clockwise direction
• and the answers are written as numbers with three digits.

Worked example 13.2: Finding a bearing

Find the bearing of from .

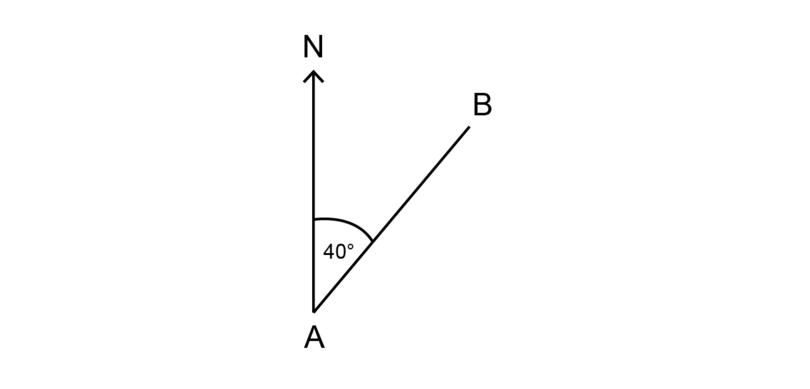
1. Step ane: Observe the North line.

   The N line is the vertical line with the label .

2. Pace 2: Mensurate in a clockwise management.

   The size of the angle is given equally .

3. Step iii: Give the bearing you have been asked for. Use iii digits in the answer.

   The begetting of from means that you lot are continuing at point and need to get to . Yous want to know what bending should be measured at betoken so that y'all tin walk in the right direction from to .

   Because has only ii digits, y'all add a in front, to show that this is a bearing. Yous also need to give the degree symbol at the end.

   The bearing of from is .

It is important to call up that to give a bearing, you always requite the bending in a clockwise direction from the North line.

Sometimes you volition be given a diagram where the angle is shown in an anti-clockwise management from the North line. Then you will need to work out what angle to give in your bearing, equally shown in the next worked example.

anti-clockwise direction Anti-clockwise is the opposite of clockwise, and so it is the direction opposite to that in which the easily of a clock (or watch) normally move.

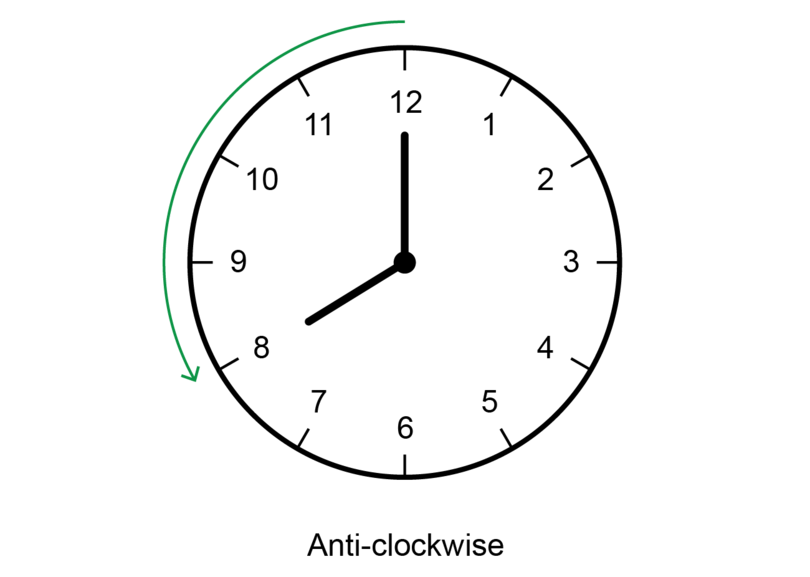
Worked instance xiii.iii: Finding a bearing when angle is given in anti-clockwise direction

Discover the bearing of from .

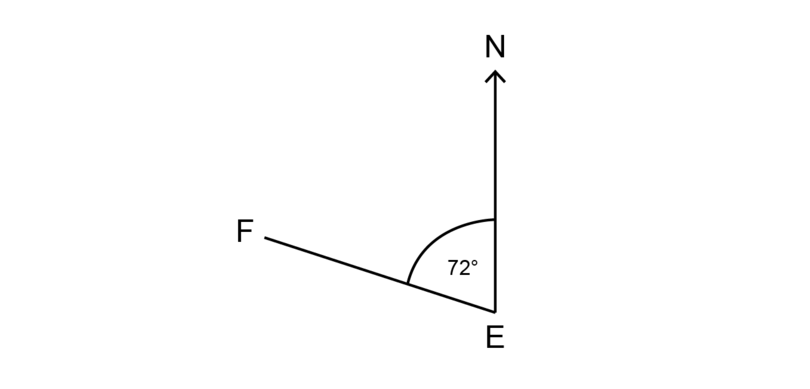
1. Step 1: Find the North line.

   The North line is the vertical line with characterization .

2. Step two: Convert the given angle to an angle measured in a clockwise direction.

   An bending of is given. This angle is measured in an anti-clockwise direction from the North line.

   To notice what that bending would be if it was measured in a clockwise direction, you lot subtract the given angle from .

   \[ \begin {align} \text{Clockwise angle} &= 360^{\circ} - 72^{\circ} (\text{revolution}) \\ & = 288^{\circ} \\ \end {align}\]

3. Step 3: Use 3 digits in the respond.

   The begetting of from is .

Find that in the worked instance in a higher place:

• The point that has "from" in front of information technology is always your starting signal. This example has "from ". Y'all desire to notice what bearing y'all must use to get from that point, to the other signal, . So you are asked for "the bearing of from
• The reason "revolution" is given in brackets. Equally in geometry, you demand to give reasons for your statements when determining bearings.

Worked instance 13.4: Finding a bearing using a straight angle

Find the begetting of from .

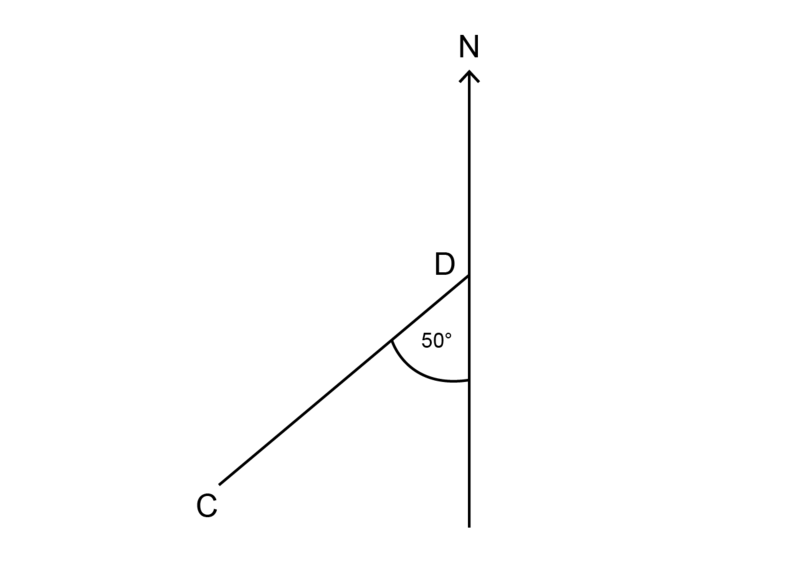
1. Step 1: Find the North line.

   The North line is the vertical line with characterization .

2. Step 2: Look carefully at how the given angle is marked.

   An angle of is given, but this angle is non measured from the Due north line.

3. Step three: Make up one's mind what the angle would be if it was measured clockwise from the North line.

   The angle is measured from the South line. The North-Southward line is a straight line. Remember that a straight line (or a straight angle) is equal to .

   To find the size of the bending from the North line, you have to add together to the given angle. Notice how this reason is given in the working below.

   \[ \begin {align} \text{Angle that gives bearing} & = 180^{\circ} + fifty^{\circ} (\text{str } \bending) \\ & = 230^{\circ} \\ \end {marshal}\]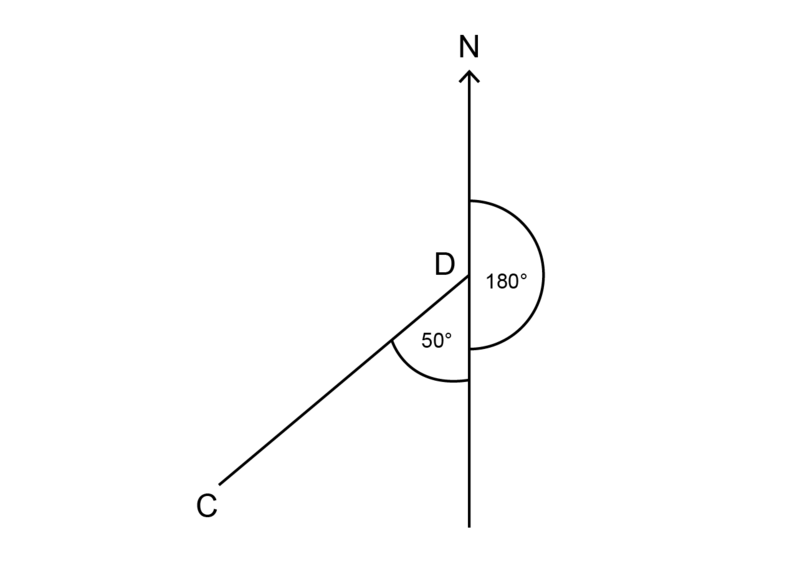

   

4. Step 4: Give the respond, using three digits for the bearing.

   The bearing of from is .

It is possible to take more than than one North line in a diagram.

Worked example 13.5 will show yous how to reason if you are given a diagram with more than one North line.

The of import thing to remember is that all North lines are parallel to each other. So you use the backdrop of parallel lines.

When two parallel lines are cut by a transversal line, the co-interior angles are supplementary. This means the co-interior angles add up to .

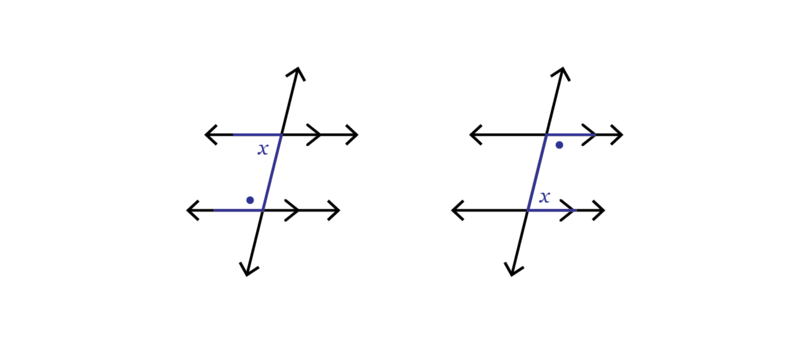
Worked case 13.5: Finding bearings when given two North lines

Using the diagram given below, find the bearing of from . So then find the begetting of from .

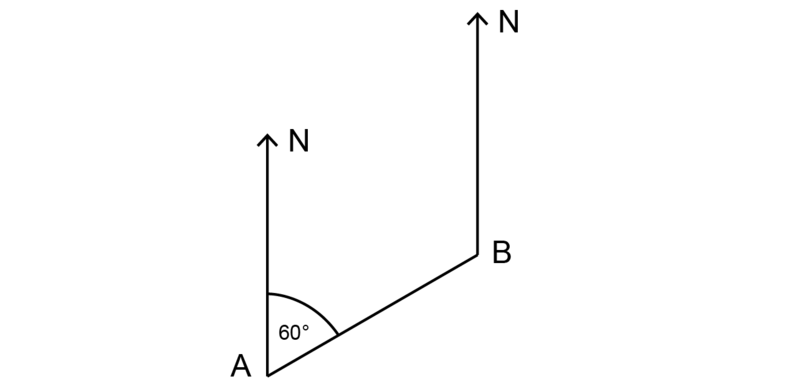
1. Stride 1: Detect the bearing of from offset.

   The diagram shows an angle of measured in a clockwise management from the North line at indicate .

2. Step two: Give the respond, using iii digits for the begetting.

   The bearing of from is .

3. Step iii: Now observe the bearing of from .

   There is a second Due north line fatigued from betoken .

   Line is at present a transversal cutting through two parallel lines (the two N lines).

   and are co-interior southward, so they are supplementary.

4. Pace 4: Find the size of the co-interior angle.

   \[ \begin {align}\\ \text{Angle at bespeak } B & = 180^{\circ} - 60^{\circ} (\text{co-int } \bending \text{s suppl; Due north lines are} \parallel)\\ & = 120^{\circ} \\ \terminate {align}\]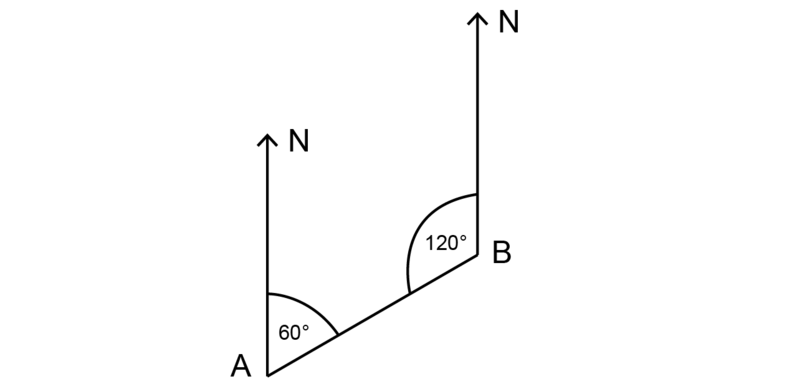

   

5. Pace 5: Detect the bending measured clockwise from the Northward line at .

   To find the bearing of from , you need to measure from the North line at . The angle of is measured anti-clockwise from this Due north line.

   To find the the angle from the North line, decrease from .

   \[ \begin {marshal}\\\ \text{Angle that gives bearing} & = 360^{\circ} - 120^{\circ} (\text{revolution})\\\ & = 240^{\circ} \\\ \end {align}\]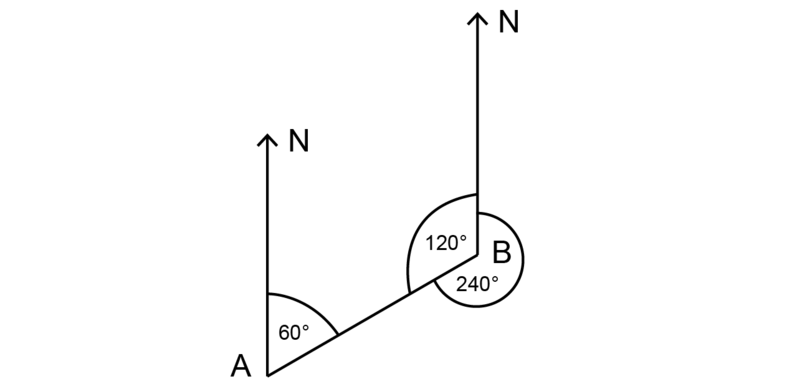

   

6. Pace half-dozen: Give the answer, using three digits for the bearing.

   The bearing of from is .

Practise xiii.2: Find bearings

1. For each diagram, write down the iii digit bearing.

   Write the respond as follows: The bearing of … from … is …

   

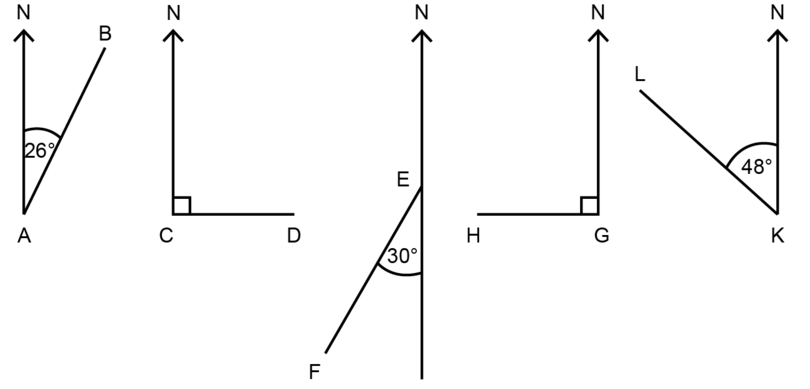
   • The begetting of from is
   • The bearing of from is
   • The bearing of from = =
   • The bearing of from = =
   • The bearing of from = =

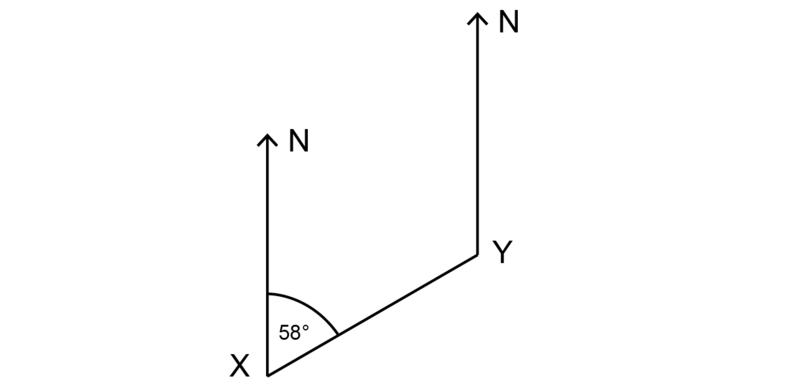
2. Apply the diagram beneath to find the bearing of from , and the begetting of from .

   

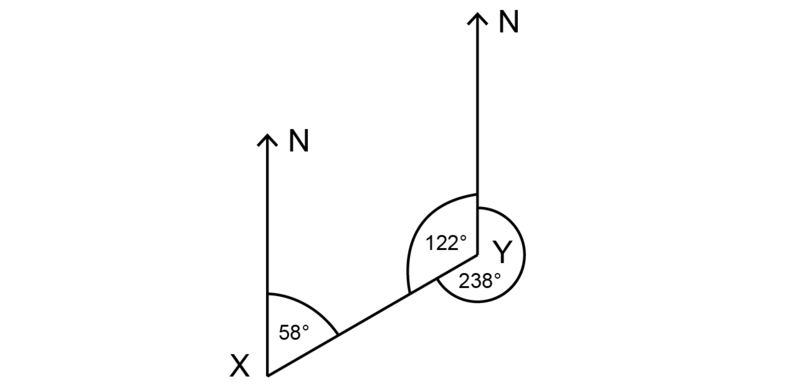
   The bearing of from is .

   To find the begetting of from , use the fact that the two North lines are parallel, so the co-interior angles are supplementary.

   \brainstorm {align}\\ \text{Co-interior angle at } Y &= 180^{\circ} - 58^{\circ} (\text{co-int } \bending \text{southward suppl; North lines }\parallel)\\ &= 122^{\circ}\\ \end {align}

   The angle at is measured in an anti-clockwise direction.

   \begin {align}\\ \text{Bending measured clockwise at } Y & = 360^{\circ} - 122^{\circ} (\text{revolution})\\ &= 238^{\circ} \\ \end {align}

   The bearing of from is .

   

3. Use the diagram beneath to find the bearing of from , and the begetting of from .

   

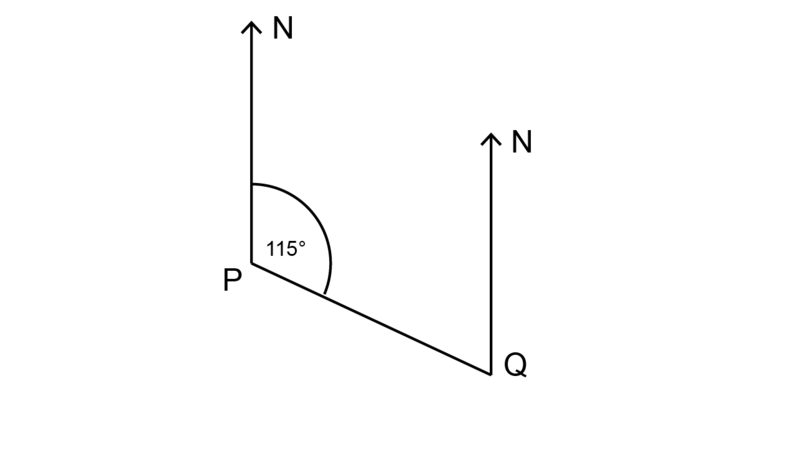
   The bearing of from is .

   To observe the bearing of from , use the fact that the ii N lines are parallel, so the co-interior angles are supplementary.

   \begin {marshal}\\ \text{Co-interior angle at } Q & = 180^{\circ} - 115^{\circ} (\text{co-int } \angle \text{s suppl; Northward lines } \parallel)\\ &= 65^{\circ} \\ \terminate {align}

   The angle at is measured in an anti-clockwise direction.

   \begin {align}\\ \text{Angle measured clockwise at } Q & = 360^{\circ} - 65^{\circ} (\text{revolution}) \\ &= 295^{\circ} \\ \end {marshal}

   The bearing of from is = .

   

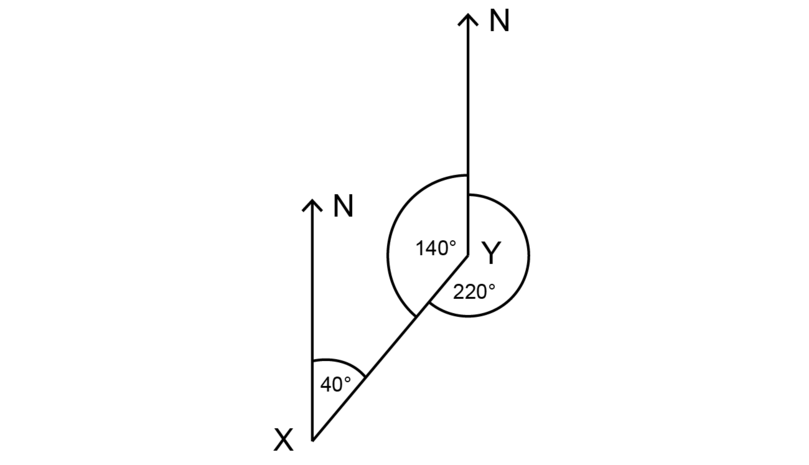
4. Use the diagram below to find the bearing of from , and the bearing of from .

   

   \brainstorm {align}\\ \text{Co-interior bending at } 10 & = 180^{\circ} - 140^{\circ} (\text{co-int } \bending \text{s suppl, North lines} \parallel)\\ &= twoscore^{\circ} \\ \stop {align}

   The bearing of from is .

   \begin {marshal}\\ \text{Angle measured clockwise at } Y & = 360^{\circ} - 140^{\circ} (\text{revolution}) \\ & = 220^{\circ} \\ \end {align}

   The begetting of from is .

   

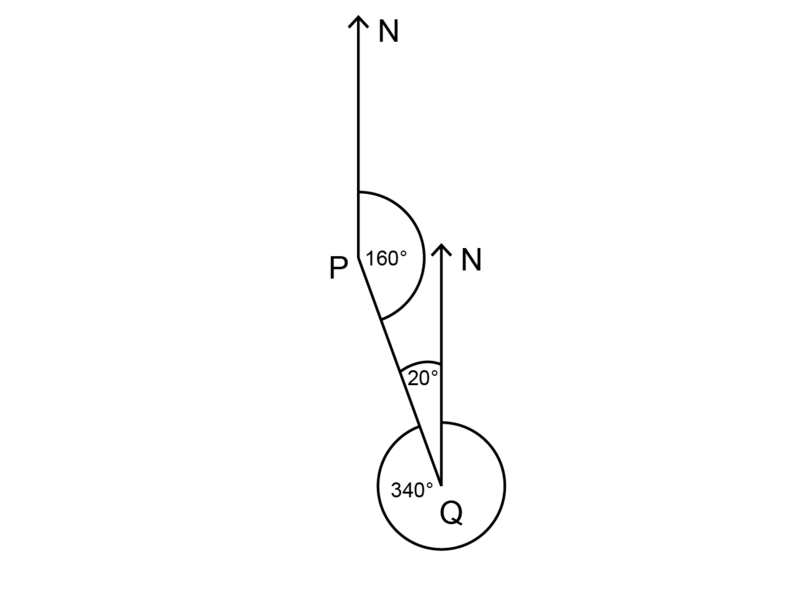
5. Use the diagram below to discover the bearing of from , and of from .

   

   \begin {align}\\ \text{Co-interior angle at } P & = 180^{\circ} - 20^{\circ} (\text{co-int } \angle \text{south suppl, N lines} \parallel)\\ &= 160^{\circ} \\ \end {align}

   The bearing of from is .

   \begin {align}\\ \text{Angle measured clockwise at } Q &= 360^{\circ} - 20^{\circ} (\text{revolution})\\ & = 340^{\circ} \\ \finish {marshal}

   The bearing of from is .

   

13.three Scale drawing and distances

A scale cartoon is a diagram in which a real object (for instance, a book, a table or a edifice) is drawn bigger or smaller while keeping the same proportions.

Architects use calibration drawings when they blueprint or plan buildings. For example, when you want to build a house yous need a flooring programme of the firm. It is not possible to describe a diagram of the floor plan of a house at its real size, of form. But if you reduce every measurement in the same proportion, and so you tin can fit the diagram onto a sheet of paper.

We tin also employ a calibration drawing together with bearing to bear witness the distances between two objects.

A scale drawing has to show clearly what ratio was used to enlarge or reduce the object. This ratio is called the scale of the drawing.

• A ratio of means that 1 unit on the calibration drawing represents ten units in real life. For example, ane cm on the scale cartoon represents x cm in real life.
• A ratio of means that 1 unit on the scale drawing represents 700 units in existent life. For example, 1 mm on the scale drawing represents 700 mm in existent life.

calibration drawing A scale drawing is a diagram of a real object where every measurement is reduced (or enlarged) in the same proportion.

scale The scale of a scale drawing tells what ratio was used to reduce (or enlarge) the dimensions of the real life object to do the scale cartoon.

Worked case 13.6: Finding a altitude using bearing and a scale drawing

On the scale drawing below, the school is at , and the clinic is at .

Describe the exact position of the clinic if a calibration of was used.

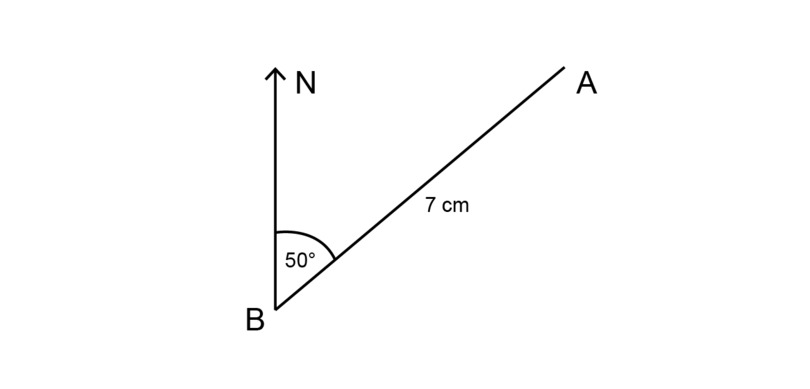
1. Step i: Read off the distance between the school and the clinic on the scale diagram.

   The diagram shows a distance of 7 cm.

2. Step two: Calculate the distance in real life.

   \begin {align}\\ \text {Distance on scale drawing} & = \text{7 cm} \\ \therefore \text{Distance in real life} & = \text{7 cm} \times 500 \\ &= \text{3,500 cm}\\ &=\text{35 metres} \end {align}

3. Footstep three: Describe the position of the clinic, giving its bearing and distance from the school.

   The clinic is 35 metres from the school, at a begetting of .

When working with bearings and scale drawings, yous may need to piece of work with the backdrop of a triangle. If you need to calculate the length of one side of a correct-angled triangle, you may apply the theorem of Pythagoras.

If is a correct-angled triangle with equal to , the theorem of Pythagoras states:

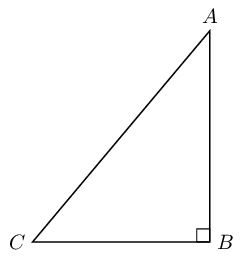
For the exercise below, remember that 100 centimetres = 1 metre, and one,000 metres = ane kilometre.

Exercise 13.3: Observe distances using bearing and calibration drawings

1. The altitude between 2 buildings, and , is shown on the scale drawing beneath.

   

   What is the distance betwixt the two buildings in existent life? Give the answer in metres.

   \begin {align}\\ \text {Distance on calibration drawing} & = \text{8.35 cm} \\ \therefore \text{Distance in real life} & = \text{8.35 cm} \times 600 \\ &= \text{5,010 cm}\\ &=\text{l.1 metres} \end {align}

2. A football player runs between two cones marked and on the diagram.

   

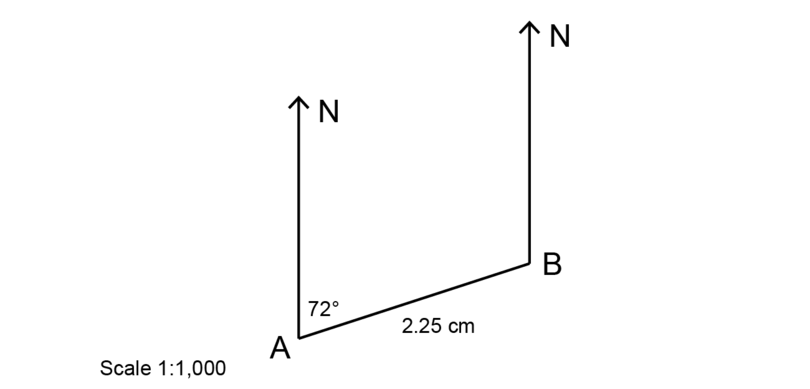
   What is the distance that the actor covers if she runs from to and then back to ? Give the respond in metres.

   \begin {marshal} \text {Altitude on scale cartoon }& = \text{2.25 cm}\\ \therefore \text{Altitude in real life } & = \text{2.25 cm} \times one,000\\ &= \text{ii,250 cm}\\ &=\text{22.v metres}\\ \finish {align} \begin {align} \text {Distance from } A \text{ to } B \text{ and and so dorsum to } A & = 2 \times 22.v \text{ metres} \\ & = 45 \text{ metres}\\ \end {align}

3. An athlete trains for an upcoming event by running from his house ( ) to work ( ) every twenty-four hour period.

   

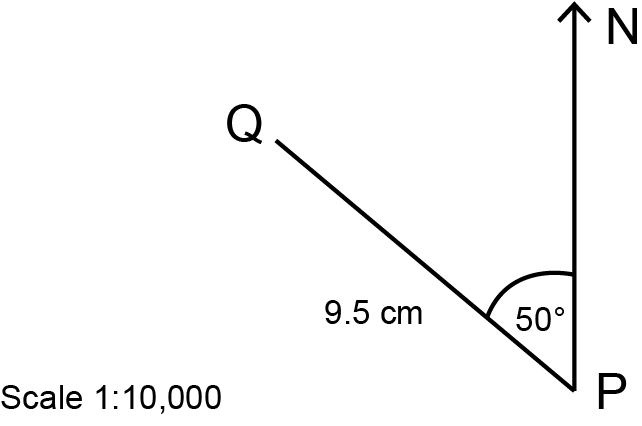
   Use the scale cartoon to describe the begetting and distance of the athlete's daily run. Give the distance in metres.

   Begetting:

   \begin {align}\\ \text{Angle measured clockwise at } P &= 360^{\circ} - 50^{\circ} (\text{revolution})\\ & = 310^{\circ} \\ \end {align}

   The bearing of from is .

   Distance:

   \begin {align} \text {Altitude on scale drawing }& {= \text{9.five cm}}\\ \therefore \text{Distance in real life } & {= \text{9.five cm} \times 10,000}\\ &= \text{95,000 cm}\\ &=\text{950 metres} \end {align}

   The athlete's daily run is 950 metres from his firm to work at a bearing of .

4. Amadi and Chidi become to the aforementioned school ( ). Amadi's business firm is at , and Chidi'southward business firm is at . The scale cartoon shows the position of the school, as well as the position of the two houses.

   

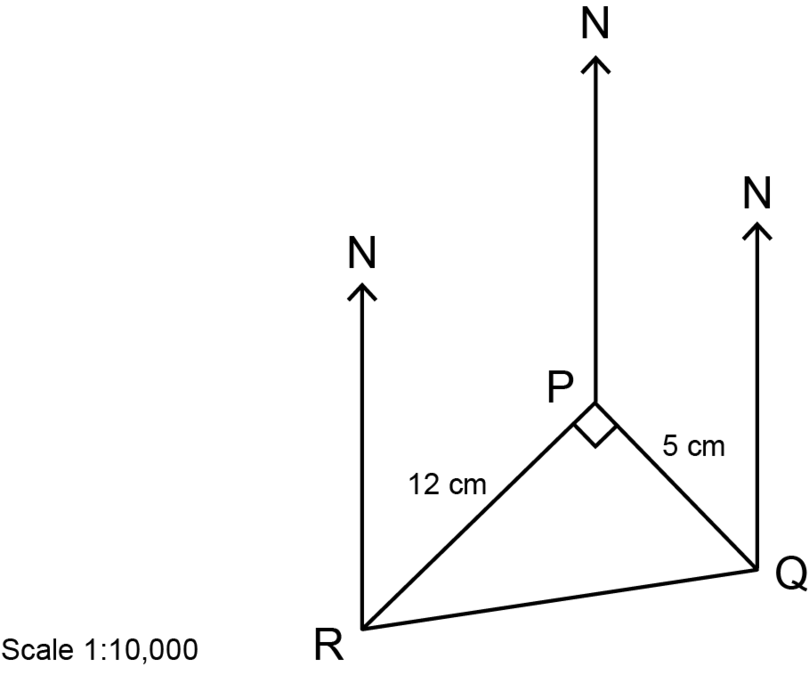
   1. What is the distance in kilometres betwixt the school and Amadi's house?

   Altitude between the school ( ) and Amadi'due south house ( ):

   \begin {align} \text {Distance on scale cartoon }& = \text{12 cm}\\ \therefore \text{Distance in existent life } & = \text{12 cm} \times 10,000\\ &= \text{120,000 cm}\\ &=\text{1,200 metres}\\ &= \text{1.2 km}\\ \cease {marshal}

   The distance from the school to Amadi'southward house is 1.ii kilometres.

   1. What is the distance in kilometres between Amadi's firm and Chidi's house?

   You will need to use the theorem of Pythagoras to discover the distance betwixt the two houses on the scale drawing.

   \brainstorm {align} QR^2 & = PR^two + PQ^2 (\text{Pythagoras}) \\ & = 5^2 + 12^two \\ & = 25 + 144\\ & = 169\\ \therefore QR & = \sqrt {169}\\ & = 13\\ \cease {marshal}

   And then, the altitude between the two houses on the scale cartoon is thirteen cm.

   \begin {align} \text {Distance on scale cartoon }& = \text{13 cm}\\ \therefore \text{Distance in real life } & = \text{thirteen cm} \times 10,000\\ &= \text{130,000 cm}\\ &=\text{one,300 metres}\\ &= \text{one.3 km}\\ \end {align}

   The altitude between Amadi'due south house and Chidi'due south firm is 1.3 kilometres.

5. In the diagram, signal shows the position of Boondocks .

   

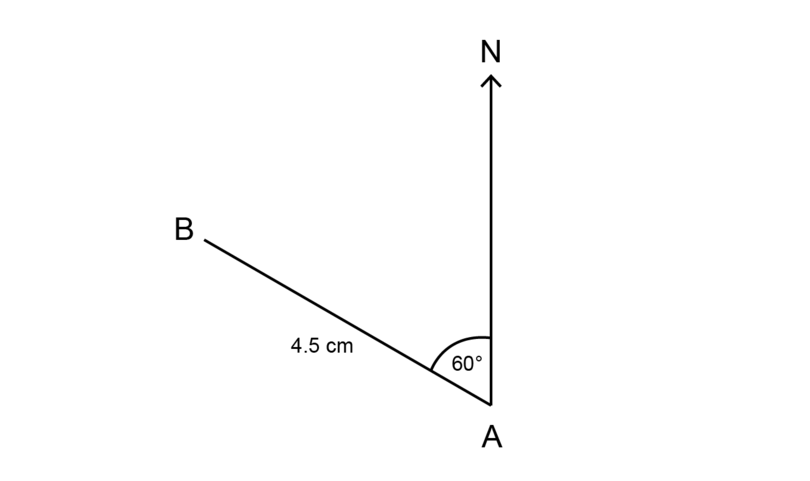
   1. Copy the diagram and complete a scale drawing to testify that Town is at a bearing of from Town . The distance between the ii towns on the scale drawing is four.5 cm.

   Remember that to construct an angle of in a clockwise direction, you accept to subtract the from . And then y'all can construct an angle in an anti-clockwise management from the North line.

   Draw an accurate calibration drawing, using the following steps:

   • Re-create the given North line and mark bespeak .
   • Use a protractor to marker an angle of in an anti-clockwise direction.
   • Construct = iv.5 cm.

   

   1. Work out the existent distance betwixt the 2 towns if the scale is . Give your reply in kilometres.

   \brainstorm {align} \text {Altitude on calibration drawing }& = \text{4.v cm}\\ \therefore \text{Altitude in existent life } & = \text{four.five cm} \times 50,000\\ &= \text{225,000 cm}\\ &=\text{two,250 metres}\\ &= \text{ii.25 km}\\ \end {marshal}

   The distance between the two towns is 2.25 kilometres.

13.4 Summary

• Bearing is a way of describing one object's position in relation to another object.
• In that location are three rules for giving a description of bearing:
  • Bearings are measured from the North line.
  • Bearings are measured in a clockwise direction.
  • Bearings are written equally numbers with three digits and a degree symbol.
• The four directions (North, South, W and Eastward) are known as the major primal points.
• There are also four minor fundamental points:
  • North-E ( ) is midway between N and Due east
  • South-East ( ) is midway between South and East
  • N-Westward ( ) is midway between North and West
  • South-West ( ) is midway between South and West.
• The begetting of from means that you are continuing at point , and you lot want to know what angle should be measured at point and so that you lot tin can walk in the right direction from to .
• Information technology is possible to have more than one N line in a diagram.
• All N lines are parallel to each other.
• When two parallel lines are cut by a transversal line, the co-interior angles are supplementary.
• Bearings can be used in a calibration drawing to show the distances betwixt ii objects.
• A calibration drawing is a diagram of a real object where every measurement is reduced (or enlarged) in the same proportion.

Source: https://www.siyavula.com/read/maths/jss2/bearing/13-bearing?id=133-scale-drawing-and-distances

Posted by: francisviode1952.blogspot.com

Share this post